Graph¶

A graph is a fundamental data structure used to represent a collection of objects and the relationships between them. It is a versatile and powerful way to model various real-world scenarios, such as social networks, transportation systems, computer networks, and more. Graphs are composed of nodes (also called vertices) and edges, where nodes represent the objects, and edges represent the connections or relationships between those objects.

Graph Concepts¶

Graphs are fundamental data structures used to represent various relationships and connections in a wide range of applications. Understanding the basic concepts related to graphs is essential for working with them effectively. This section introduces key graph-related terms and concepts.

Vertices/Nodes¶

A vertex or node is a fundamental element in a graph. It represents an entity or an object within the graph. Each vertex may have associated properties, and in some cases, a degree is used to describe the number of edges connected to a vertex.

Edges/Arcs¶

An edge or arc is a connection between two vertices in a graph, representing a relationship or association between them. Edges can have different characteristics:

Directed: In a directed graph (also known as a digraph), edges have a specific direction, indicating that there is a one-way relationship from one vertex to another.
Undirected: In an undirected graph, edges do not have a direction, signifying a bidirectional relationship between vertices.
Weighted: Edges can be weighted, meaning they have associated numerical values or weights that represent the cost, distance, or strength of the relationship.

Connectivity¶

Connectivity refers to how vertices in a graph are connected to each other. Several concepts related to connectivity include:

Path Between Two Vertices: A path is a sequence of edges that connect two vertices. The length of a path is determined by the number of edges it contains.
Distance Between Two Vertices: The distance between two vertices is the length of the shortest path connecting them.
Adjacent: Two vertices are said to be adjacent if there is an edge connecting them directly.
Connected: A graph is considered connected if there is a path between any pair of vertices. Otherwise, it is unconnected.
Cyclic: A graph is cyclic if it contains at least one cycle, which is a closed path that returns to the same vertex without repeating any edge.
Acyclic: A graph is acyclic if it does not contain any cycles.

Graph Properties¶

Graphs can possess various properties that define their characteristics. Some of the key graph properties include:

Directed/Undirected: A graph can be classified as directed if it contains directed edges, and undirected if it contains undirected edges.
Weighted/Unweighted: Graphs can be weighted if they have edges with associated weights, or unweighted if all edges have equal weight.
Cyclic/Acyclic: Graphs can be cyclic if they contain cycles, or acyclic if they do not have any cycles.
Connected/Unconnected: A graph can be connected if there is a path between all pairs of vertices, or unconnected if there are isolated components without connections.
Dense/Sparse: A graph can be dense if it has a large number of edges relative to the number of vertices, or sparse if it has relatively few edges.

Note

For undirected graph, only outgoing edges are counted when working with degree, path, distance, cycle, connectivity, and so on.

Examples¶

digraph G {
node[shape=circle];
a -> {b, c, d};
b -> {a, d};
} — Directed connected cyclic graph¶

graph G {
node[shape=ellipse];
Atlanta -- Dallas [label=4];
Atlanta -- Miami [label=4];
Atlanta -- Orlando [label=3];
Dallas -- Austin [label=1];
Dallas -- Orlando [label=6];
} — Undirected connected cyclic weighted graph¶

graph G {
node[shape=circle];
b -- a;
a -- {c, d};
b -- {e, f};
} — Undirected connected acyclic graph (Tree)¶

digraph G {
rankdir=LR;
node[shape=box];
task1 -> task2;
task2 -> {task3, task4};
task3 -> {task5, task6};
task4 -> task6;
} — Directed acyclic graph (DAG) task planning¶

Representations¶

Unlike linked list, and tree, graph are seldom represented using nodes and pointers due to the complexity of the data structure. Instead, graph are represented using one of the following methods:

Example undirected graph:

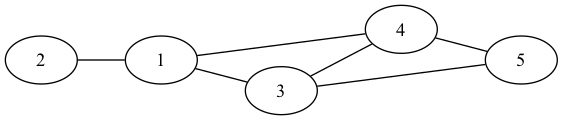
Undirected graph¶
List of edges

A list of edges is a 1d array in which every element in the array represents an edge. It is the simplest way to represent a graph. It is also an easy way to store a graph in a relational database. It is not efficient for most graph algorithms though.

n1

n2

1

2

1

3

1

4

3

4

3

5

4

5
Adjacency list

An adjacency list is a 1d array in which every element in the array represents a vertex and points to a list of its neighbors.

Adjacency list¶
Adjacency matrix

An adjacency matrix is a 2d array in which each row represents a source vertex and each column represents a destination vertex. The elements in the matrix represents the edge between the two vertices.

The matrix will be symmetric for undirected graph.

Adjacency Matrix¶

1

2

3

4

5

1

0

1

1

1

0

2

1

0

0

0

0

3

1

0

0

1

1

4

1

0

1

0

1

5

0

0

1

1

0

Complexity¶

Assume that we have a graph with \(V\) vertices and \(E\) edges. The average number of neighbors is \(N\). For a full graph: \(N = V - 1; E=V(V-1)/2\). For a sparse matrix, \(N << V; E << V(V-1)/2\).

Adjacency list vs Adjacency Matrix¶
	List of edges	Adjacency list	Adjacency matrix
Space Complexity	\(\Theta(E)\)	\(\Theta(V*N)\)	\(\Theta(V*V)\)
Time to check adjacency	\(\Theta(E)\)	\(\Theta(N)\)	\(\Theta(1)\)
Time to find all neighbors	\(\Theta(E)\)	\(\Theta(N)\)	\(\Theta(V)\)

Graph Traversal¶

Depth-first search (DFS)

Starting from one vertex, visit all vertices along the path started from the starting vertex till then end of the path (no unvisited neighbors) and then backtrack.
- iterative using a stack
- recursive
Breadth-first search (BFS)

Starting from one vertex, visit all other vertices in the order of the distances to the starting vertex.
- iterative using a queue

Graph Glossary¶

Vertex/Node (Graph)¶: Entities that are interconnected
Edge/Arc (Graph)¶: The connection between two vertices
Adjacency¶: Two vertices are adjacent if connected by an edge
Neighbors (Graph)¶: All vertices that are adjacent
Path (Graph)¶: A sequence of edges from one vertex to another
Length of path (Graph)¶: The number of edges along a path
Distance (Graph)¶: The length of the shortest path between two vertices
Full graph¶: A graph in which all vertices are connected to other vertices
Sparse graph¶: A graph in which the number of edge is way fewer than the number for a full graph with the same number of vertices
Directed graph¶: A graph in which every edge has a direction from one vertex to another
Undirected graph¶: A graph in which every edge is symmetric
Cyclic Graph¶: A graph in which you can always find at least a path that starts and ends on a same vertex
Acyclic Graph¶: Can not find any path that starts and ends on a same vertex
Weighted graph¶: A graph in which every edge has a weight
Depth-first search (DFS, Graph)¶: Starting from one vertex, visit all vertices along the path started from the starting vertex till then end of the path (no unvisited neighbors) and then backtrack.
Breadth-first search (BFS)¶: Starting from one vertex, visit all other vertices in the order of the distances to the starting vertex.