Data Structure and Algorithm Design II

Sections

• Dynamic Programming

• Max Sum Subarray Problem

• Chain Matrix Multiplication Problem

• Longest Common Subsequence Problem

Dynamic Programming

Overview

• An algorithmic paradigm

• Break into overlapping subproblems

• Only calculate once to avoid repeated work

• Store the result in a table for future use

Characteristics

• What makes a problem suitable for dynamic programming?

  • Optimal substructure

  • Overlapping subproblems

• Implementation techniques:

  • Memoization/tabulation

  • Recursive formulation

  • Either top-down or bottom-up

Problems Solved by DP

• Enumeration, decision or optimization types of problems

• Fibonacci numbers

• Max subarray sum (Kadane’s algorithm)

• Matrix chain multiplication

• Longest common subsequence

• Knapsack problem

• Integer partition

• Coin change

• Rod cutting

Benefit and Challenges

Complexity Analysis

Max Sum Subarray

• Given an array of integers, find the contiguous subarray with the largest sum. The array can contain both negative and positive values.

• For array \([-2, -3, 4, -1, -2, 1, 5, -3]\), the contiguous subarray with the largest sum is \([4, -1, -2, 1, 5]\) with sum 7.

• Many real-life applications

  • Stock market

  • Image processing

  • Bioinformatics

• Problem type: Optimization

• Need exact solution

• Satisfies

  • Optimal substructure

  • Overlapping subproblems

• Solutions

  • Brute-force \(\Theta(n^2)\)

  • Divide and conquer \(\Theta(n \log n)\)

  • Dynamic Programming (Kadane’s algorithm) \(\Theta(n)\)

Brute-force Solutions

• Consider all possible subarrays and compute their sums

function brute_force_max_subarray(arr):
  max_sum = -infinity

  for start from 0 to length(arr) - 1:
    sum_of_subarray = 0

    for end from start to length(arr) - 1:
      sum_of_subarray = sum_of_subarray + arr[end]

      if sum_of_subarray > max_sum:
        max_sum = sum_of_subarray

  return max_sum

Divide and Conquer Solution

• Divide the array into two halves

• Recursively find the maximum subarray sum in:

  • Left half

  • Right half

  • Crossing the midpoint

function max_subarray(arr, low, high):
  if low == high:
    return arr[low]

  mid = (low + high) / 2
  return max(max_subarray(arr, low, mid),
            max_subarray(arr, mid + 1, high),
            max_crossing_sum(arr, low, mid, high))

Divide and Conquer Solution (cont.)

function max_crossing_sum(arr, low, mid, high):
  left_sum = -infinity
  sum = 0
  for i from mid downto low:
    sum = sum + arr[i]
    if sum > left_sum:
        left_sum = sum

  right_sum = -infinity
  sum = 0
  for j from mid + 1 to high:
    sum = sum + arr[j]
    if sum > right_sum:
        right_sum = sum

  return left_sum + right_sum

Dynamic Programming Solution

• Kadane’s algorithm

• Idea: Compute the maximum subarray sum ending at each position

• At each end position, the maximum subarray sum is either:

  • The maximum subarray sum ending at the previous position plus the current element

  • The current element

• Scan the array from left to right only once

Dynamic Programming Solution (cont.)

Consider the array \([-2, 1, -3, 4, -1, 2, 1, -5, 4]\):

• Start with \(current\_max = arr[0] = -2\) and \(global\_max = -2\).

• At the second element (1), \(current\_max\) is \(max(-2+1, 1)\), which is 1. \(global\_max\) is now \(max(-2, 1)\), which is 1.

• This process continues, updating \(current\_max\) and \(global\_max\) with each new element.

• By the end of the array, \(global\_max\) contains the maximum sum, which in this case is 6 from the subarray \([4, -1, 2, 1]\).

Dynamic Programming Solution (cont.)

function kadane_algorithm(arr):
  current_max = global_max = arr[0]

  for index from 1 to length(arr) - 1:
    current_max = max(arr[index], current_max + arr[index])

    global_max = max(global_max, current_max)

  return global_max

Chain Matrix Multiplication Problem

Overview

• Given a sequence of matrices, find the most efficient way to multiply these matrices together.

• The costs are different depending on how you associate the matrices in the multiplication.

• Problem type: Optimization

• Need exact solution

• Satisfies

  • Optimal substructure

  • Overlapping subproblems

• Solutions

  • Brute force

  • Dynamic programming

Example

• Consider the multiplication of four matrices A, B, C, and D with dimensions \(10 \times 30\), \(30 \times 5\), \(5 \times 60\), and \(60 \times 10\), respectively. We can fully parenthesize the product in five distinct ways:

  1. \(((AB)C)D\)

  2. \((A(BC))D\)

  3. \((AB)(CD)\)

  4. \(A((BC)D)\)

  5. \(A(B(CD))\)

• The cost of 3 is the best:

  1. \((10 \times 30 \times 5) + (10 \times 5 \times 60) + (10 \times 60 \times 10) = 1500 + 3000 + 6000 = 10500\)

  2. \((30 \times 5 \times 60) + (10 \times 30 \times 60) + (10 \times 60 \times 10) = 9000 + 18000 + 6000 = 33000\)

  3. \((10 \times 30 \times 5) + (5 \times 60 \times 10) + (10 \times 5 \times 10) = 1500 + 3000 + 500 = 5000\)

  4. \((30 \times 5 \times 60) + (30 \times 60 \times 10) + (10 \times 30 \times 10) = 9000 + 18000 + 3000 = 30000\)

  5. \((5 \times 60 \times 10) + (30 \times 5 \times 10) + (10 \times 30 \times 10) = 3000 + 1500 + 3000 = 7500\)

Brute Force Solution

• The combinatorics: The way to parenthesize a product of \(n\) matrices is \(\Theta(\frac{4^n}{n^{3/2}\sqrt{\pi}})\). A.k.a. the Catalan number.

• The complexity is close to exponent complexity.

• The algorithm is not practical.

Dynamic Programming Solution

• Bottom-up approach

  • Let the length of chain \(L\) range from 2 to \(n\).

  • Enumerate all subchains of length \(L\) in the sequence.

  • Enumerate all possible ways of parenthesizing each subchain by splitting the subchain into two subchains.

  • Time complexity: \(\Theta(n^3)\)

• Memorization using two tables

  • \(m[i, j]\): The minimum number of scalar multiplications needed to compute the matrix \(A_i \cdots A_j\).

  • \(s[i, j]\): The index \(k\) at which we split the product \(A_i \cdots A_j\) in an optimal parenthesization \(A_i \cdots A_k A_{k+1} \cdots A_j\).

  • Both \(\Theta(n^2)\) space.

Dynamic Programming Algorithm (cont.)

• C++ example that only computes the cost

int matrixChainOrder(int p[], int n) {
  int m[n][n];

  for (int i = 1; i < n; i++)
    m[i][i] = 0;

  // L is the chain length
  for (int L = 2; L < n; L++) {
    for (int i = 1; i < n - L + 1; i++) {
      int j = i + L - 1;
      m[i][j] = INT_MAX;
      // Try all possible split points
      for (int k = i; k <= j - 1; k++) {
        int q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
        if (q < m[i][j])
          m[i][j] = q;
      }
    }
  }
  // Return the minimum number of scalar multiplications needed
  // to multiply the original chain
  return m[1][n - 1];
}

Longest Common Subsequence (LCS) Problem

• Sequences and subsequences: foundational concepts in computational problems

• Critical for sequence comparison in bioinformatics and computer science

  • DNA sequence alignment

  • DNA sequence similarity

  • Text comparison and plagiarism detection

  • File comparison

  • Version control systems

LCS Problem Overview

• LCS: finding the longest subsequence common to two sequences

  • More than one possible solution

  • Subsequence: not necessarily contiguous

• Used in genetics and version control systems

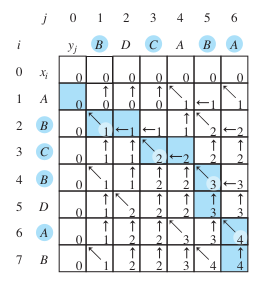
• Example: The Longest Common Subsequence for the DNA sequences “AGGTAB” and “GXTXAYB” is “GGTAB”

LCS Problem Properties

• Optimal Substructure: (last character match version)

  • For sequences X and Y, if X[m] equals Y[n], the LCS includes X[m] and is one more than LCS(X[1..m-1], Y[1..n-1]).

    • E.g. LCS(“ABCBDAB”, “BDCABB”) = 1 + LCS(“ABCBDA”, “BDCAB”)

  • If X[m] does not equal Y[n], the LCS is the longer of LCS(X[1..m], Y[1..n-1]) or LCS(X[1..m-1], Y[1..n]).

    • E.g. LCS(“ABCBDAB”, “BDCABD”) = max(LCS(“ABCBDAB”, “BDCAB”), LCS(“ABCBDA”, “BDCABD”))

• Overlapping Subproblems:

  • Calculating LCS(X[1..m], Y[1..n]) will often require recalculating LCS(X[1..m-1], Y[1..n-1]), LCS(X[1..m], Y[1..n-1]), and LCS(X[1..m-1], Y[1..n]) multiple times.

Brute Force Approach

• Involves comparing all possible subsequences of both strings and compare

• Results in exponential time complexity \(2^{m+n}\)

• Not feasible for long sequences due to inefficiency

Divide and Conquer Approach

• Employ the subproblem definition of LCS

• Recursively divide the problem into smaller subproblems

• Redundant computations on overlapping subproblems

function findLCSLength(s1, s2, m, n):
    // Base case: If either of the strings is empty, LCS length is 0
    if m == 0 or n == 0:
        return 0

    // If the last characters of both strings match
    if s1[m-1] == s2[n-1]:
        return 1 + findLCSLength(s1, s2, m-1, n-1)

    // If the last characters of both strings don't match
    return max(findLCSLength(s1, s2, m, n-1), findLCSLength(s1, s2, m-1, n))

Dynamic Programming (DP) Solution

• DP Table: set up with dimensions one greater than sequence lengths

• Matching characters: increment LCS length

• Non-matching characters: take the maximum value from adjacent cells

• LCS length located at dp[m][n]

• Algorithm complexity: \(\Theta(m*n)\) for both time and space

Traceback for LCS

Credit: Introduction to Algorithms, 4th Ed., T. Cormen et al.

• Can only find one LCS

• Reconstruct LCS from the filled DP table

• Backtrack from dp[m][n], storing characters

• Diagonal movement for matches; otherwise to cell with higher value; if same, go up

• Complexity: \(\Theta(m+n)\)

• Question: How about same values?

Pseudocode

Function LCS(X, Y):
    m = length of X
    n = length of Y
    dp = array of (m+1) rows and (n+1) columns

    # Initialize the table with 0's, as the LCS of an empty sequence
    # with any sequence is 0
    For i from 0 to m:
        dp[i][0] = 0
    For j from 0 to n:
        dp[0][j] = 0

    # Fill the dp table
    For i from 1 to m:
        For j from 1 to n:
            If X[i] == Y[j]:
                dp[i][j] = dp[i-1][j-1] + 1
            Else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])

    # The length of LCS is in the cell dp[m][n]
    length_LCS = dp[m][n]

Pseudocode (cont.)

# To find the LCS string, traceback from dp[m][n]
LCS = ""
i = m, j = n
While i > 0 and j > 0:
    If X[i] == Y[j]:
        LCS = X[i] + LCS  # Prepend the character to LCS
        i = i - 1
        j = j - 1
    Else If dp[i-1][j] >= dp[i][j-1]: # if same, go up
        i = i - 1
    Else:
        j = j - 1

Return LCS, length_LCS

Variations

• All LCSs: The DP solution only finds one LCS. To find all LCSs, use backtracking to find all possible paths in the DP table that lead to the LCS length.

• Longest Common Substring: A substring is a contiguous sequence of characters within a string. The Longest Common Substring (LCSu) problem is similar to the LCS problem, but requires that the common elements be contiguous.

• Improve space complexity: The DP solution requires \(\Theta(m*n)\) space. This can be improved to \(\Theta(min(m, n))\) by only storing the current and previous rows of the DP table.