Data Structure and Algorithm Design II
Module 7
Xingang (Ian) Fang
Sections
Solving Recurrences
Solving Recurrence
Outline
Overview
Recurrence Relations
Solving Recurrence Relations
Substitution Method
Recursion Tree Method
Master Method
Overview
Solving recurrence is a process of finding a closed form expression for a given recurrence relation that is usually employed to describe the time function of a recursive algorithm.
Note: It is usually simplified to find the big theta rather than the exact close form expression.
Algorithms that are recursive in nature are usually described by recurrence relations.
Tower of Hanoi
Merge Sort
Fibonacci Numbers
Recurrence Relations
A recurrence relation is an equation that recursively defines a sequence, where each term is a function of one or more of the preceding terms.
E.g. \(T(n) = 2T(n/2) + \Theta(n)\) for merge sort
The goal of “solving a recurrence” is to obtain a closed form expression for \(T(n)\) that does not involve any recurrence.
E.g. \(T(n) = \Theta(n \log n)\) for merge sort
This is a very challenging math problem but in computer science we are only interested in some certain patterns of recurrence relations.
Depending on the algorithms there are some common recurrence relations employed in the analysis of algorithms.
Common Forms of Recurrence Relations
Divide and conquer Recurrence
\(T(n) = aT(n/b) + f(n)\)
Merge sort
Binary search
Maximum subarray
Strassen’s matrix multiplication
First order linear Recurrence
\(T(n) = aT(n-1) + f(n)\)
Linear search (recursive version)
Insertion sort/Selection sort (recursive version)
Euclidean’s GCD algorithm
Second order linear Recurrence
\(T(n) = aT(n-1) + bT(n-2) + f(n)\)
Fibonacci numbers (naive recursive version)
Note: the \(f(n)\) term is usually simplified to big Theta notation.
Solving Recurrence Relations
Finding a closed form expression for a given recurrence relation is a challenging math problem.
In computer science we are only interested in some certain patterns.
Three methods:
Substitution method
Recursion tree method
Master method
Substitution Method
Two steps
Guess the close form of the solution
Guess a general form of the solution
Use substitution to refine the formula (optional)
Use mathematical induction to prove the guess is correct
Note: You do not need to understand the details of the math. Focus on the overall idea and the process.
Example: Guessing the Close Form
Start from the recurrence relation: \(T(n) = T(n-1) + 3n\) and \(T(1)=1\).
Guess the solution is \(T(n) = An^2 + Bn + C\) where \(A\), \(B\), \(C\) are constants.
Use substitution to find \(A\), \(B\), \(C\).
\[\begin{split}\begin{align*} T(n) &= T(n-1) + 3n \\ An^2 + Bn + C &= A(n-1)^2 + B(n-1) + C + 3n \\ An^2 + Bn + C &= An^2 - 2An + A + Bn - B + C + 3n \\ An^2 + Bn + C &= An^2 + (-2A + B + 3)n + (A - B + C) \\ \end{align*}\end{split}\]So, we have the following equations:
\[\begin{split}\begin{align*} A &= A \\ B &= -2A + B + 3 \text{} \\ C &= A - B + C \\ f(1) &= A + B + C = 1 \\ \end{align*}\end{split}\]Solve them to get \(A = 1.5\), \(B = 1.5\), \(C = -2\).
The final formula is \(T(n) = 1.5n^2 + 1.5n - 2\).
Example: Proof by Mathematical Induction
For the recurrence relation: \(T(n) = T(n-1) + 3n\) and \(f(1)=1\).
To prove the formula \(T(n) = 1.5n^2 + 1.5n - 2\) is correct for all \(n\).
Base case: \(T(1) = 1.5 + 1.5 - 2 = 1\). Correct!
If the formula is correct for \(n-1\), then
\[\begin{split}\begin{align*} T(n) &= T(n-1) + 3n \\ &= 1.5(n-1)^2 + 1.5(n-1) - 2 + 3n \\ &= 1.5n^2 - 3n + 1.5 + 1.5n - 1.5 - 2 + 3n \\ &= 1.5n^2 + 1.5n - 2 \\ \end{align*}\end{split}\]So, the formula is correct for \(n\).
Done!
Recursion Tree Method
A graphical visualization to assist the guessing of the closed form.
Steps
Draw the recursion tree
Sum up the cost of each level
Sum up the cost of all levels
E.g. \(T(n) = 3T(n/4) + \Theta(n^2)\)
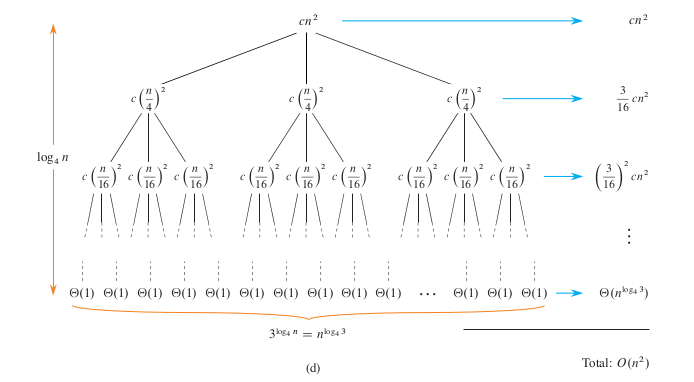
Credit: Introduction to Algorithms, 4th Ed., T. Cormen et al.
Master Method
A general method to solve recurrences of the form:
\[T(n) = aT(n/b) + f(n)\]where \(a \geq 1\), \(b > 1\) and \(f(n)\) is an asymptotically positive function.
\(n\) is the problem size.
\(a\) is the number of recursive calls.
\(n/b\) is the size of each subproblems where \(b\) is the size reduction factor.
\(f(n)\) is the cost of dividing the problem and combining the solutions.
This is the well-known divide-and-conquer form of recurrence.
Based on Master Theorem.
Three Cases
Case 1: If \(f(n) = O(n^c)\) where \(c < \log_b a\), then: \(T(n) = \Theta(n^{\log_b a})\)
Case 2: If \(f(n) = \Theta(n^{\log_b a} \cdot \log^k n)\) for a \(k \geq 0\), then: \(T(n) = \Theta(n^{\log_b a} \cdot \log^{k+1} n)\)
Case 3: If \(f(n) = \Omega(n^c)\) where \(c > \log_b a\), and if \(a f\left(\frac{n}{b}\right) \leq k f(n)\) for some \(k < 1\) and sufficiently large \(n\), then: \(T(n) = \Theta(f(n))\)
Intuitions: The amount of work done in each recursive call is smaller, same level, or larger than the cost of recursive calls.
Examples
For the recurrence relation of the Merge Sort algorithm:
\(T(n) = 2T\left(\frac{n}{2}\right) + \Theta(n)\)
We have:
\(a = 2\)
\(b = 2\)
\(f(n) = \Theta(n) = \Theta(n^1 \times \log ^0 n)\)
Using the Master Method:
\(\log_b a = \log_2 2 = 1\)
\(f(n) = \Theta(n^1 \times \log ^0 n)\)
This falls under Case 2 with \(k = 0\). Thus, the solution is: \(T(n) = \Theta(n \log n)\)