Data Structure and Algorithm Design II
Chapter 3
Xingang (Ian) Fang
Sections
Tree data structures
Binary search trees
Self-balancing Trees
AVL trees
Tree Data Structure
Xingang (Ian) Fang
Outline
Definitions
Tree Concepts
Applications
Operations
Implementation variations
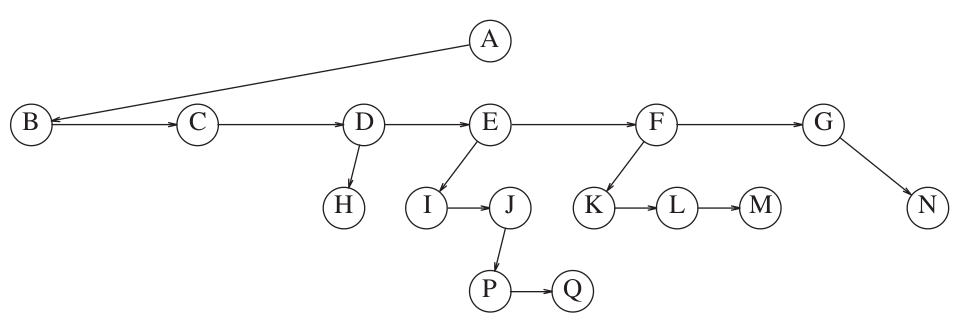
Binary tree
Definitions
In graph theory, a tree is a connected and acyclic undirected graph.
focus on connectivity and acyclicity
In computer science, a tree is a hierarchical data structure composed of nodes connected by edges, where each node has a parent (except for the root node) and zero or more children.
focus on hierarchy and parent-child relationship
Recursive definition: root and subtrees, each of which is also a tree
Tree Concepts
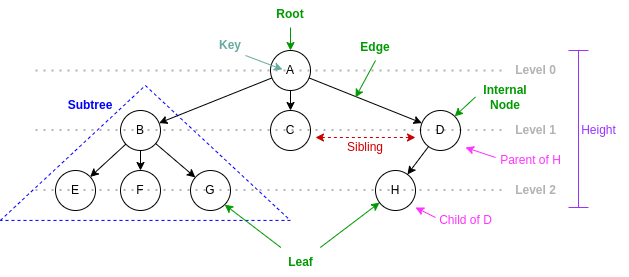
Concepts: root, internal node, leaf, edge, subtree, sibling, parent, child, level, height
Other Concepts
Degree of a node or a tree
Depth
Ancestor and descendant
Path
Distance
Ordered Unordered
Applications
File system (directory, sub-directory, and file)
Decision making (decision tree)
Indexing (binary search tree, B-tree)
Parsing tree
Heap (complete binary tree)
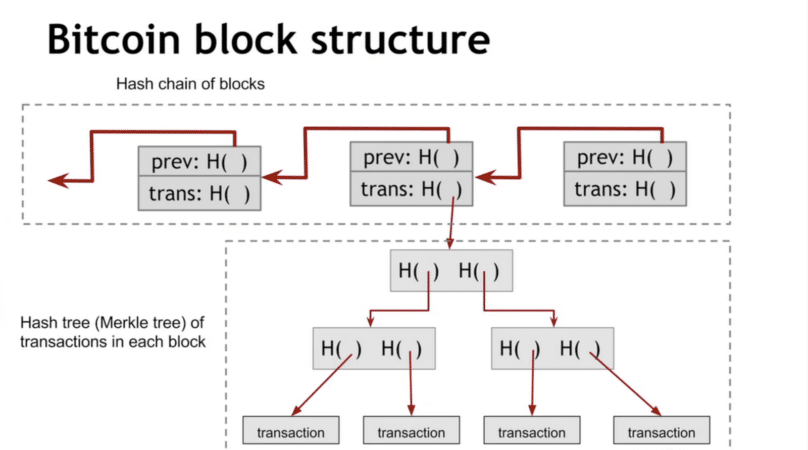
Blockchain (Merkle tree)
Search-based Artificial Intelligence (game tree)
Operations
Search
Insertion
Deletion
Traversal
Breadth-first traversal
Depth-first traversal
Pre-order traversal
Post-order traversal
Height
Degree
Implementation Variations
Each node stores a variable-length list of references to child nodes
Each node stores a reference to its first child and a reference to its next sibling
Each node stores a reference to its parent
First child next sibling representation
Credit: Data Structures and Algorithm Analysis in C++, 4th Edition. Mark Allen Weiss.
Binary Tree
Only concepts and operations that are different from general trees are covered.
Definition: Degree 2 ordered tree.
Concepts:
Left child and right child
Operations:
In-order traversal
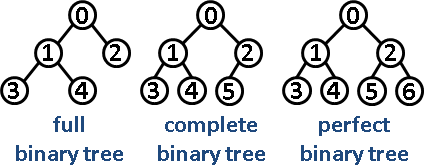
Variations:
Full binary tree
Complete binary tree
Perfect binary tree
Binary Search Tree
Xingang (Ian) Fang
Outline
Definition
Behaviors
Implementation
Drawbacks
Applications
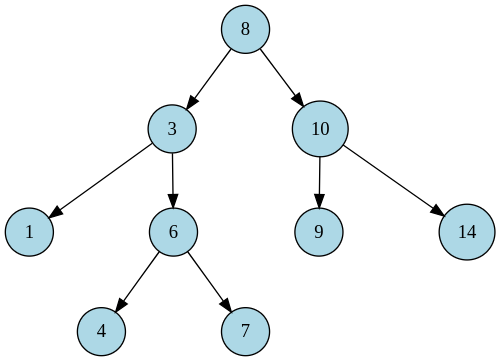
Definition and Behaviors
Definition A binary search tree (BST) is a binary tree, in which for every node, its left child has a smaller or equal key than itself while its right child has a greater or equal key than itself.
Behaviors
Insertion
Deletion
Search
Traversal
In-order traversal: left subtree, root, right subtree
Ascending ordered output
Implementation
Algorithms that happens from top to bottom
Easy to implement either iteratively or recursively
search
insert
Algorithms that happens from bottom to top
Easy to implement recursively; Hard to implement iteratively (must use stack)
subtree removal (may be used in the destruction of a tree)
find min node or find max node (part of remove)
in-order traversal
pre-order traversal
Implementation (cont’d)
Search
if equal, found
if smaller, search left subtree
if greater, search right subtree
Insertion
if equal, do nothing
if smaller, insert to left subtree
if left is empty, insert
if greater, insert to right subtree
if right is empty, insert
Removal
remove leaf node: simply remove it
remove node with one child: replace the node with its child
remove node with two children
find the min node in the right subtree (successor)
replace the node to be removed with the min node
remove the min node (min node has at most one child)
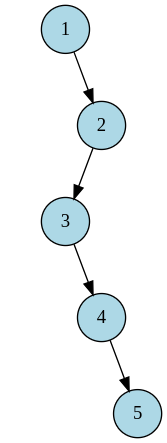
Drawbacks of naive BST
Algorithm efficiency depends on the average height of the BST
BST may degrade a very unbalanced form or even to a linked list
Solution 1: randomize the order of insertion
Solution 2: add balancing mechanism
Self-balancing
External balancing
Solution 3: move the most recently accessed node toward the root
Only optimize the search performance for a specific access pattern
No guarantee for the worst case
Splay tree
Applications
Indexing: store a set of references to records in a BST and use the key as the search key.
Tree Sort: sort a sequence of elements by building a BST and then traversing it in-order.
Tree Map: store a set of (key, value) pairs in a BST and use the key as the search key.
Tree Set: store a set of elements in a BST and use the element as the search key.
Self-balancing Trees
Xingang (Ian) Fang
Outline
Overview
Variations
Overview
Definition: A self-balancing tree is a type of tree data structure in which the balance or height of the tree is automatically adjusted during insertions and deletions to ensure that the tree remains reasonably balanced.
Motivation: To overcome the potential performance issues that can occur in trees due to unbalanced structures.
Alternative approach: External balancing on general trees.
Variations
BST family
AVL tree
Balance factor: height(left subtree) - height(right subtree)
Balance factor of each node is either -1, 0, or 1.
Insertion and deletion may trigger a balance operation.
Balance operations achieved by rotations.
Red-black tree (FYI)
A BST implementation of 2-3 tree (Algorithm, 4th Ed.) or 2-3-4 tree (older versions).
Each node is colored red or black.
Insertion and deletion may trigger adjustment.
Adjustment achieved by a re-color or a rotation.
B-tree family
B-tree (B tree, not B minus tree)
varying but bounded number of children per node
always balanced
maintain balance by redistributing keys among nodes
2-3 tree is a B-tree with 2 or 3 children per node
B+ tree (FYI)
B* tree (FYI)
AVL Tree
Xingang (Ian) Fang
Outline
Overview
Implementation details
Overview
Definition: An AVL (Adelson-Velsky and Landis) tree is a self-balancing binary search tree data structure. It is designed to maintain a balanced tree structure at all times, ensuring that the height difference (balance factor) between the left and right subtrees of any node is limited to no more than one.
Worst case guarantee for search, insert, and delete is \(\Theta(\log n)\)
Characteristics
Balance factor = height(left subtree) - height(right subtree)
Balance factor of 0, -1, or 1 is considered balanced
Insertion and deletion operations may cause the tree to become unbalanced, in which cases the balance factor of one or more nodes will be -2 or +2.
Self-balancing: balance restored by rotations during insertion and deletion
Balancing operations are performed bottom-up, starting with the deepest unbalanced node.
Self-balancing in AVL Trees
Find and restore the imbalance from bottom up
Check the balance factor of each node.
If the balance factor is -2 or +2, perform rotations to restore balance.
4 types of imbalances and corresponding restoration by rotations
Type of Imbalances
Balance factor of -2 or +2 indicates an imbalance
Go to the longest subtree from top to bottom starting from the unbalanced node
Always refer to the lowest unbalanced node first. The higher unbalanced nodes may be fixed automatically when the lower ones are fixed.
Naming convention for imbalances:
Left-Left (LL)
Right-Right (RR)
Left-Right (LR)
Right-Left (RL)
Rotations to restore balance
Left rotation to restore right-right (RR) imbalance.
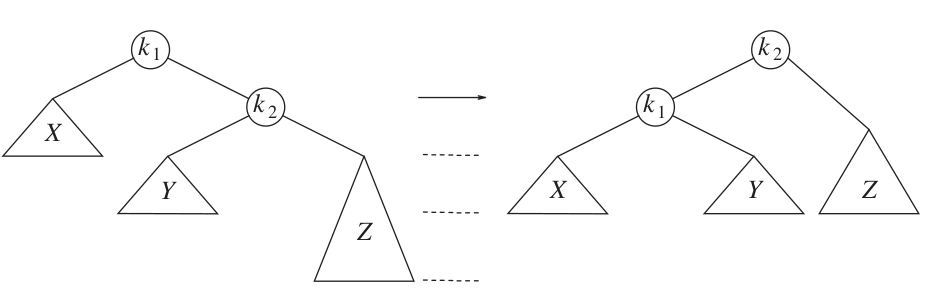
Right rotation to restore left-left (LL) imbalance.
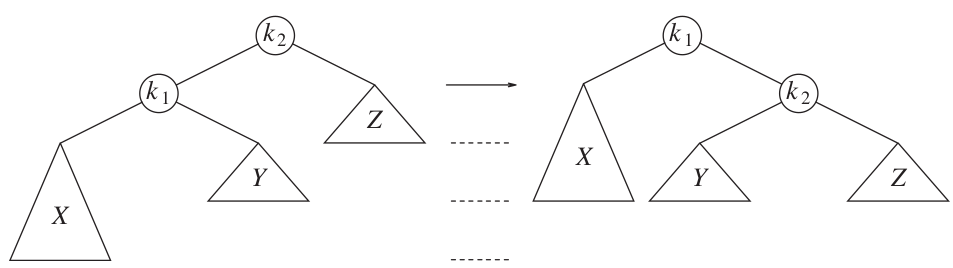
Credit: Data Structures and Algorithm Analysis in C++, 4th Edition. Mark Allen Weiss.
Rotations to restore balance (cont.)
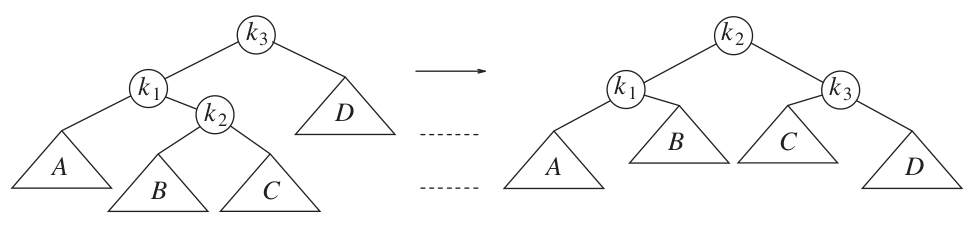
Double rotations are named from the bottom up. E.g., Left-Right rotation means first a left rotation on the left child, then a right rotation on the unbalanced node.
Left-right double rotation to restore left-right (LR) imbalance.
Right-left double rotation to restore right-left (RL) imbalance.
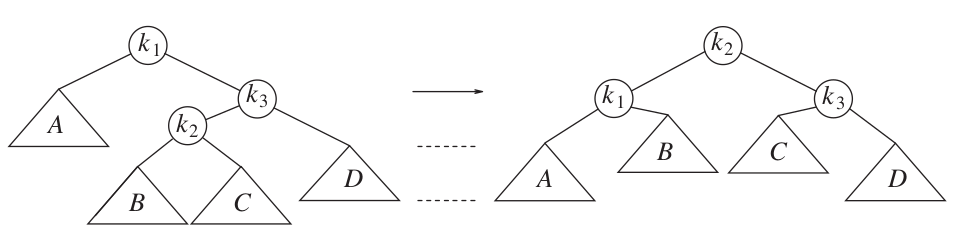
Credit: Data Structures and Algorithm Analysis in C++, 4th Edition. Mark Allen Weiss.
What to remember
What is the imbalance type?
LL: Right rotation
RR: Left rotation
LR: Left-right double rotation
RL: Right-left double rotation