Combinatorics And Counting¶
Overview¶
Combinatorics is a branch of mathematics that deals with counting, arrangement, and combination of objects. It is about finding ‘how many’ possible structures of a certain kind exist. Combinatorics provides tools to answer questions like:
How many ways can a set of objects be arranged?
How many combinations or selections can be made from a group?
Significance¶
Combinatorics is important in computer science because it is the mathematical foundation for many algorithms and data structures. Combinatorics can be used to:
Analyze the complexity of algorithms
Design efficient algorithms
Develop data structures that can efficiently store and retrieve data
Solve problems in cryptography, machine learning, and other areas of computer science
Counting Principles¶
The Sum Rule:
If an event can occur in m ways and another event can occur in n ways, and the two events are mutually exclusive (meaning that they cannot both occur at the same time), then the total number of ways that either event can occur is m+n.
Example: If you are allowed to choose one from 3 shirts and 4 pants, then you have a total of \(3+4=7\) different pieces of clothing to choose from.
The Product Rule:
If an event can occur in m ways and another event can occur in n ways, both events should happen as the same time, and the two events are independent (meaning that the occurrence of one event does not affect the probability of the other event occurring), then the total number of ways that both events can occur is \(m \times n\).
Example: Using the same clothing example, if you want to decide on an outfit combination of one shirt and one pants out of the 3 shirts and 4 pants, then you have \(3×4=12\) possible combinations to choose from.
The Division Rule:
If out of the total n ways of doing something, every item is counted m times, then the number of different ways of doing that thing is n/m. This is a method to correct consistent overcounting.
Example: If you count n edges of a polygon by starting vertex and ending vertex, then each edge is counted twice. So, the number of edges is n/2.
Include-exclude principle
The Inclusion-Exclusion Principle is a counting technique used to compute the number of elements in the union of several sets. This principle helps to correct the overcounting that occurs when using just the sum of the sizes of individual sets.
Two sets \(|A \cup B| = |A| + |B| - |A \cap B|\)
Three sets \(|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |A \cap C| + |A \cap B \cap C|\)
Pigeonhole principle
If n items are put into m containers, with \(n>m\), then at least one container must contain more than one item.

Recurrence relations
Count sub-problems and combine the results to get the final answer.
Category of problems¶
Arrangement
Ordering and organizing objects
Permutation (order matters)
standard
all objects: \(P^n = n!\)
r objects: \(P^n_r = \frac{n!}{(n-r)!}\)
circular
all objects: \((n-1)!\)
r objects: \(C^n_r \times (r-1)!\)
allow repetition
r objects: \(n^r\)
multi-set
all objects with multiple duplicate sets
\(\frac{n!}{n_1!n_2!...n_k!}\)
Selection (order does not matter)
Selecting objects from a set
Order does not matter
Combination
Find permutation first, then divide by r! to correct overcounting
standard \(C^n_r = \frac{n!}{r!(n-r)!}\)
allow repetition \(\frac{(n+r-1)!}{r!(n-1)!}\)
Subset
Number of all subsets \(2^n\)
\(\sum_{k=0}^n C^n_k = 2^n\)
Distribution (Partition)
Distributing objects into groups
Distributing n identical objects into r distinct groups
\(C^{n+r-1}_n\)
Distributing n distinct objects into r distinct groups
\(r^n\)
Integer partition - represent integer n as sum of positive integers (value up to k)
\(p(n,k) = p(n,k-1) + p(n-k,k)\)
recursive algorithm
hard to find closed form solution in math
Geometric counting
Catalan numbers
Correct Overcounting In Selection¶
Example. Select 3 letters from A, B, C, D. Order does not matter.
To solve the problem a good strategy is to first find the number of permutations and then divide by the number of ways to arrange the 3 letters.
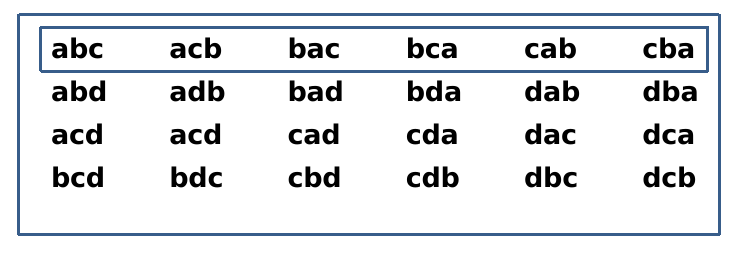
Each row represent all permutations of a unique combination. As each row have \(3!\) permutations, using the division rule, we can correct the overcounting.
The final result is \(C^4_3 = P^4_3/P^3_3 = 4\).
Some Strategies¶
Direct counting
Break down into cases
sum - exclusive events
product - independent events
Counting by complement
\(Count = Total - \overline{Count}\)
Counting by recursion
May resort to an algorithm
Solve Combinatorics Problems¶
Steps¶
Identify the type of problem
Arrangement
Selection
Distribution/Partition
Identify the constraints
Repetition
Order
Grouping
Identify the counting principle
Ron’s Greasy Spoon¶
Definition: Build your own breakfast from the menu:
1 egg dish 4 choices: Scrambled, Fried, Poached, Omelette
2 sides 5 choices: Bacon, Sausage, Hash Browns, Toast, Pancakes
1 drink 4 choices: Coffee, Tea, Milk, Orange Juice
How many different breakfasts can you order?
Solution:
Product rule: choose 1 egg dish, 2 sides, 1 drink, independent events
Choose 1 egg dish: 4 ways
Choose 2 sides: \(C^5_2 = 10\) ways
Choose 1 drink: 4 ways
Total number of breakfasts: \(4 \times 10 \times 4 = 160\)
More Arrangement/Selection Problems¶
How many 8 bit strings start with either 110 or 101?
Sum rule: select two 5 bit strings, exclusive to each other
For each: size 5 permutation with repetition \(2^5\)
Total: \(2^5 + 2^5 = 64\)
Six person committee { a, b, c, d, e, f}. Select President, Vice President, and Treasurer and either a or b must be President. Each person can have only one role.
Product rule: Select 3 roles, independent events
Order matter? Yes, President, Vice President, Treasurer are different roles
President: 2 choices
Vice President: 4 choices (anyone but President)
Treasurer: 3 choices (anyone but President and Vice President)
Anagram¶
An anagram of a string is another string that contains the same characters, possibly in a different order. For example, “listen” can be rearranged to form “silent” or “enlist”, making them anagrams.
Question: How many anagrams of the word “mississippi” are there?
Order matters: permutation
Repetition: 4 i’s, 4 s’s, 2 p’s
Division rule to correct overcounting
E.g. The order of the 4 i’s does not matter, so divide by 4!
Total number of anagrams: \(\frac{11!}{4!4!2!} = 34650\)
How many ways to give 5 gifts of the same type to 3 children?¶
This is a partition problem to distribute 5 identical items to 3 distinct bins.
The well-known method called “star and bar”:
The idea is to put 5 items (*) together with 2 separators (|) in a line like: * * * | * *|.
Out of the total 7 positions, pick 5 positions to put the stars.
A less efficient method is to use the sum rule and break down into cases. Calculate the number of ways for various partitions of 5 items into 3 bins. Like 5-0-0, 4-1-0, 3-2-0, 3-1-1, etc. Then add them up.
Poker Game¶
To find number of possible hands when you draw 5 random cards.
Total number of possible hands:
5 cards from 52 cards
\(C^{52}_5 = 2598960\)
Royal flush: 1 each suit, 4 total
Straight flush: 36 ways
5 consecutive cards, same suit
Select starting card from Ace, 2, … to 10 10 ways per suit: \(C^{10}_{1}\)
Select suit: \(C^{4}_{1}\)
Remove over counting: royal flush
Four of a kind: 624 ways
Select 2 ranks (order matters): \(P^{13}_2\)
Select a suite for 1 rank: \(C^{4}_{1}\)
Full house: 3744 ways
Select 2 ranks from 13 ranks (order matters) \(P^{13}_{2}\)
Select 3 suits for the 3 cards: \(C^{4}_{3}\)
Select 2 suits for the 2 cards: \(C^{4}_{2}\)
Flush: 5108 ways
Select 5 ranks from 13 ranks: \(C^{13}_5\)
Select a suit: \(C^{4}_{1}\)
Remove overcounting: straight flush, royal flush
Straight 10200 ways
Product rule
Select the starting card: \(C^{10}_1\)
Select the suits for each card (repetition allowed) : \(4^5\)
Remove overcounting: straight flush, royal flush
Three of a kind: 54912 ways
Product rule
Select a rank for 3 cards: \(C^{13}_{1}\)
Select the suits for 3 cards: \(C^{4}_{3}\)
Select 2 ranks for the other 2 cards: \(C^{12}_2\)
Select the suits for the other 2 cards: \(4^2\)
Two pairs: 123552 ways
Product rule
Select 2 ranks for the pairs: \(C^{13}_2\) ways
Select 1 rank for the other card: \(C^{11}_1\) ways
Select 2 suits for the first pair: \(C^{4}_{2}\) ways
Select 2 suits for the second pair: \(C^{4}_{2}\) ways
Select 1 suit for the other card: \(C^{4}_{1}\) ways
One pair 1,098,240 ways (exercise)
High card
Hard to count directly because of the many cases of overcounting
Use complement: Total - all other hands
Poker Game: Partial Hands¶
Rule of thumb:
Anything you do not know is assumed to be equally likely to be any of the remaining cards.
With two spades in hand? How many ways to get a flush?
3 spades in the remaining 11 spades
\(C^{11}_3 = 165\)
Two Aces in hand? How many ways to get a full house?
Case 1: 1 Ace and a pair
Select 1 Ace (2 left): \(C^{2}_{1}\)
Select 1 rank for the pair: \(C^{12}_1\)
Select 2 suits for the pair: \(C^{4}_{2}\)
Case 2: 3 of a kind
Select 1 rank for the 3 of a kind: \(C^{12}_1\)
Select 3 suits for the 3 of a kind: \(C^{4}_{3}\)
Add the two cases because they are exclusive