Longest Common Subsequence Problem¶
Introduction¶
Sequence Comparison¶
Sequences and subsequences are foundational concepts in the study of computational problems. A sequence is an ordered list of elements, while a subsequence is a series of elements that appear in the same order as in the original sequence but not necessarily consecutively. Sequence comparison is a critical operation in various domains such as bioinformatics, where it is used to align DNA sequences, and in computer science for text comparison and file differencing tools.
LCS Problem¶
The Longest Common Subsequence (LCS) problem is a classic computer science challenge. It involves finding the longest sequence of elements that are common and in the same order in two given sequences without necessarily being contiguous. This problem has practical applications in areas such as genetics, where it can be used to identify similar regions of DNA between species, and in version control systems to identify changes between file versions.
An example of the LCS problem can be illustrated with two sequences, “ABCBDAB” and “BDCABC”. The LCS for these sequences is “BCAB”.
Optimal Substructure¶
For sequences X and Y, if X[m] equals Y[n], the LCS includes X[m] and is one more than LCS(X[1..m-1], Y[1..n-1]).
E.g. LCS(“ABCBDAB”, “BDCABB”) = 1 + LCS(“ABCBDA”, “BDCAB”)
If X[m] does not equal Y[n], the LCS is the longer of LCS(X[1..m], Y[1..n-1]) or LCS(X[1..m-1], Y[1..n]).
E.g. LCS(“ABCBDAB”, “BDCABD”) = max(LCS(“ABCBDAB”, “BDCAB”), LCS(“ABCBDA”, “BDCABD”))
Overlapping Subproblems¶
Calculating LCS(X[1..m], Y[1..n]) will often require recalculating LCS(X[1..m-1], Y[1..n-1]), LCS(X[1..m], Y[1..n-1]), and LCS(X[1..m-1], Y[1..n]) multiple times.
Brute Force Approach¶
A naive method to find the Longest Common Subsequence is to compare all subsequences of the first sequence against all subsequences of the second sequence. This brute force approach examines every possible pair of subsequences, which results in exponential time complexity \(2^{m+n}\). Due to its inefficiency, particularly with long sequences, this method is impractical for real-world applications where time and computational resources are factors to consider.
Divide and Conquer Approach¶
The divide-and-conquer solution to the Longest Common Subsequence (LCS) problem leverages the concept of breaking down the problem into smaller subproblems. It begins by employing the subproblem definition of LCS, where the LCS of two strings is found by considering the LCS of their substrings. The algorithm recursively divides the original problem into smaller subproblems by examining characters from the end of the two input strings. When the last characters of the strings match, it incrementally builds the LCS length and continues with shorter substrings. If the last characters do not match, it explores both possibilities: removing the last character from one of the strings and keeping the other intact, selecting the longer LCS length among these alternatives. This divide-and-conquer approach effectively explores all possible combinations and ultimately returns the length of the LCS for the entire input strings.
This approach still computes redundant subproblems, which results in a time complexity of \(\Theta(2^n)\).
function findLCSLength(s1, s2, m, n):
// Base case: If either of the strings is empty, LCS length is 0
if m == 0 or n == 0:
return 0
// If the last characters of both strings match
if s1[m-1] == s2[n-1]:
return 1 + findLCSLength(s1, s2, m-1, n-1)
// If the last characters of both strings don't match
return max(findLCSLength(s1, s2, m, n-1), findLCSLength(s1, s2, m-1, n))
DP Solution for LCS¶
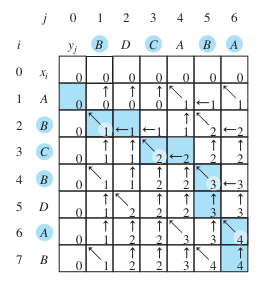
DP Table: Create a table with rows and columns corresponding to the lengths of the two sequences being compared plus one. The extra row and column are used to store the LCS length for subsequences of length 0.
Cell Values:
If the current characters match, dp[i][j] = dp[i-1][j-1] + 1.
If not, dp[i][j] is the maximum of dp[i-1][j] or dp[i][j-1].
LCS Length: The length of the LCS is found at dp[m][n], where m and n are the lengths of the sequences.
Complexity: The algorithm runs in \(\Theta(m*n)\) time and requires \(\Theta(m*n)\) space.
Traceback to Find the LCS¶
Can only find one LCS
After the DP table is filled, the LCS is not immediately apparent; it must be constructed by a traceback process.
Starting from i = m, j = n, move backwards through the table dp:
If the characters at i in string 1 and j in string 2 match, they are part of the LCS. Store this character. Move diagonally to dp[i-1][j-1].
If they don’t match, move up to dp[i-1][j] or left to dp[i][j-1] cell, whichever has a higher value.
The traceback continues until it reaches dp[0][0], reconstructing the LCS in reverse.
Credit: Introduction to Algorithms, 4th Ed., T. Cormen et al.
Pseudocode¶
Function LCS(X, Y):
m = length of X
n = length of Y
dp = array of (m+1) rows and (n+1) columns
# Initialize the table with 0's, as the LCS of an empty sequence
# with any sequence is 0
For i from 0 to m:
dp[i][0] = 0
For j from 0 to n:
dp[0][j] = 0
# Fill the dp table
For i from 1 to m:
For j from 1 to n:
If X[i] == Y[j]:
dp[i][j] = dp[i-1][j-1] + 1
Else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# The length of LCS is in the cell dp[m][n]
length_LCS = dp[m][n]
# To find the LCS string, traceback from dp[m][n]
LCS = ""
i = m, j = n
While i > 0 and j > 0:
If X[i] == Y[j]:
LCS = X[i] + LCS # Prepend the character to LCS
i = i - 1
j = j - 1
Else If dp[i-1][j] > dp[i][j-1]:
i = i - 1
Else:
j = j - 1
Return LCS, length_LCS
Variations¶
All LCSs: The DP solution only finds one LCS. To find all LCSs, use backtracking to find all possible paths in the DP table that lead to the LCS length.
Longest Common Substring: A substring is a contiguous sequence of characters within a string. The Longest Common Substring (LCSu) problem is similar to the LCS problem, but requires that the common elements be contiguous.
Improve space complexity: The DP solution requires Theta(m*n) space. This can be improved to \(\Theta(min(m, n))\) by only storing the current and previous rows of the DP table.