Greedy Solution to Huffman Coding Problem

Huffman Coding

Huffman coding is a lossless data compression algorithm. The idea is to assign variable-length codes to input characters, lengths of the assigned codes are based on the frequencies of corresponding characters. The most frequent character gets the smallest code and the least frequent character gets the largest code.

Characteristics

• Prefix code (a.k.a Prefix-free code)

  • No codeword appears as a prefix of any other codeword.

  • No ambiguity when decoding a bitstream.

    For example, if ‘a’ is encoded as ‘01’, ‘b’ cannot be encoded as ‘0’. Otherwise, when decoding ‘01’, it is ambiguous whether it is an ‘a’ (01) or a ‘b’ (0) followed by something (1).

• Optimal code

  • Minimizes the length of the encoded bitstream.

  • The most frequent character are encoded with the least number of bits.

Applications

As a fundamental algorithm in data compression, Huffman coding is used in various compression schemes such as JPEG, MP3, and DEFLATE (PKZIP). It is also used in other algorithms or applications that require lossless compression and depression like in network transmission software.

Prefix Coding Tree

The coding tree is a binary tree that represents the mapping between characters and their corresponding codewords.

• Full binary tree

• Leaf nodes are characters (guaranteed prefix code)

• Each internal node means a bit in the codeword

Example coding trees

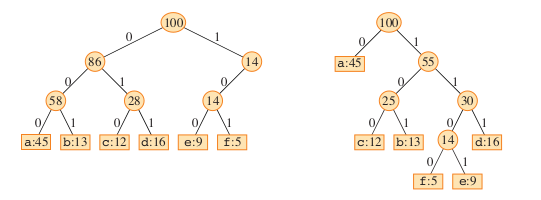
Credit: Introduction to Algorithms, 4th Ed., T. Cormen et al.

• Left: Fixed length encoding

  • Total space: 3 * (45 + 13 + 12 + 16 + 9 + 5) = 300 bits

• Right: Huffman coding

  • Total space: 1 * 45 + 3 * (13 + 12 + 16) + 4 * (9 + 5) = 224 bits

• Contents in nodes:

  • Leaf node: <character>: <frequency>

  • Internal node: <total frequency of the subtree>

Algorithm to build a Huffman coding tree

This is a greedy algorithm that builds the tree bottom-up from the least frequent characters to the most frequent characters.

• Create a leaf node for each symbol and add it to the min priority priority queue.

• While there is more than one node in the min priority queue:

  • Dequeue two nodes with the lowest frequencies from the min priority queue

  • Create a new internal node with these two nodes as its children and with frequency equal to the sum of the two nodes’ frequency

  • Add the new node to the min priority queue

• The remaining node is the root node and the tree is complete

Credit: Pseudo-code adopted from Wikipedia

Steps to build the example tree

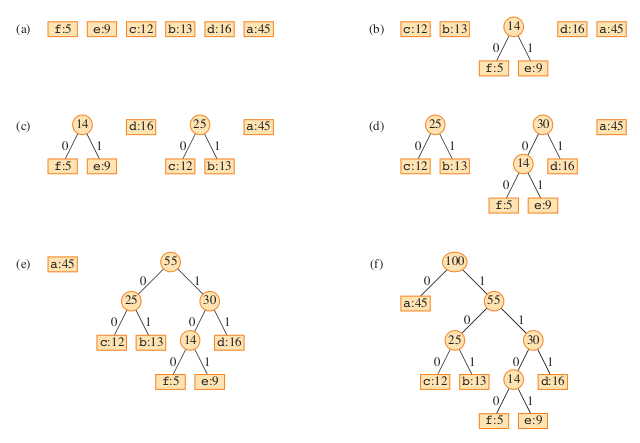
Credit: Introduction to Algorithms, 4th Ed., T. Cormen et al.