Graph

Concepts

  • Vertex/Node

    • degree

  • Edge/Arc

    • directed

    • undirected

    • weighted

  • Connectivity

    • path between two vertices

      • length

    • distance between two vertices

    • adjacent

    • connected

    • cyclic

    • acyclic

  • Graph properties

    • directed/undirected

    • weighted/unweighted

    • cyclic/acyclic

    • connected/unconnected

    • dense/sparse

Examples

digraph G { node[shape=circle]; a -> {b, c, d}; b -> {a, d}; }

Directed connected cyclic graph

graph G { node[shape=ellipse]; Atlanta -- Dallas [label=4]; Atlanta -- Miami [label=4]; Atlanta -- Orlando [label=3]; Dallas -- Austin [label=1]; Dallas -- Orlando [label=6]; }

Undirected connected cyclic weighted graph

graph G { node[shape=circle]; b -- a; a -- {c, d}; b -- {e, f}; }

Undirected connected acyclic graph (Tree)

digraph G { rankdir=LR; node[shape=box]; task1 -> task2; task2 -> {task3, task4}; task3 -> {task5, task6}; task4 -> task6; }

Directed acyclic graph (DAG) task planning

Representations

For the undirected graph:

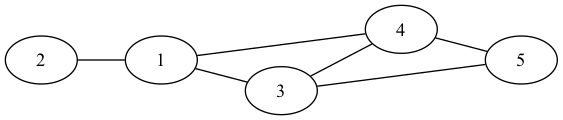
graph g1 { rankdir=LR; 1 -- 3, 4; 2 -- 1; 3 -- 4, 5; 4 -- 5; }

Undirected graph

  • List of edges

    A list of edges is a 1d array in which every element in the array represents an edge. It is the simplest way to represent a graph. It is also an easy way to store a graph in a relational database. It is not efficient for most graph algorithms though.

    1

    2

    1

    3

    1

    4

    3

    4

    3

    5

    4

    5

  • Adjacency list

    An adjacency list is a 1d array in which every element in the array represents a vertex and points to a list of its neighbors.

    digraph ll { rankdir=LR; node [shape=record]; first[label="<f1> 1|<f2> 2|<f3> 3|<f4> 4|<f5> 5", height=5]; a1 [label="{ <data> 2 | <ref> }"]; b1 [label="{ <data> 3 | <ref> }"]; c1 [label="{ <data> 4 | <ref> }"]; a2 [label="{ <data> 2 | <ref> }"]; a3 [label="{ <data> 1 | <ref> }"]; b3 [label="{ <data> 4 | <ref> }"]; c3 [label="{ <data> 5 | <ref> }"]; a4 [label="{ <data> 1 | <ref> }"]; b4 [label="{ <data> 3 | <ref> }"]; c4 [label="{ <data> 5 | <ref> }"]; a5 [label="{ <data> 3 | <ref> }"]; b5 [label="{ <data> 4 | <ref> }"]; first:f1 -> a1:data:w; a1:ref:c -> b1:data; b1:ref:c -> c1:data; first:f2 -> a2:data:w; first:f3 -> a3:data:w; a3:ref:c -> b3:data; b3:ref:c -> c3:data; first:f4 -> a4:data:w; a4:ref:c -> b4:data; b4:ref:c -> c4:data; first:f5 -> a5:data:w; a5:ref:c -> b5:data; }

    Adjacency list

  • Adjacency matrix

    An adjacency matrix is a 2d array in which each row represents a source vertex and each column represents a destination vertex. The elements in the matrix represents the edge between the two vertices.

    Adjacency Matrix

    _

    1

    2

    3

    4

    5

    1

    0

    1

    1

    1

    0

    2

    1

    0

    0

    0

    0

    3

    1

    0

    0

    1

    1

    4

    1

    0

    1

    0

    1

    5

    0

    0

    1

    1

    0

Graph Traversal

  • Depth-first search (DFS)

    Starting from one vertex, visit all vertices along the path started from the starting vertex till then end of the path (no unvisited neighbors) and then backtrack.

    • iterative using a stack

    • recursive

  • Breadth-first search (BFS)

    Starting from one vertex, visit all other vertices in the order of the distances to the starting vertex.

    • iterative using a queue

Algorithms

Minimum spanning tree

This algorithm generates a tree that connects all connected vertices in a graph with the minimum total edge weight. See visualization

  • Prim’s algorithm

  • Kruskal’s algorithm

Dijkstra’s shortest path

Among the many variations of the shortest path algorithms, single-source shortest path algorithm is most commonly discussed. The objective is to find the shortest path of all other vertices to given a vertex (source). Shortest path problem with unweighted graph can be solved using BFS. Dijkstra’s approach works with weighted (non-negative weight) graph. See visualization

  • invented by Edsger Dijkstra

  • employs a priority queue ADT

Graph Glossary

Vertex/Node (Graph)

Entities that are interconnected

Edge/Arc (Graph)

The connection between two vertices

Adjacency

Two vertices are adjacent if connected by an edge

Neighbors (Graph)

All vertices that are adjacent

Path (Graph)

A sequence of edges from one vertex to another

Length of path (Graph)

The number of edges along a path

Distance (Graph)

The length of the shortest path between two vertices

Full graph

A graph in which all vertices are connected to other vertices

Sparse graph

A graph in which the number of edge is way fewer than the number for a full graph with the same number of vertices

Directed graph

A graph in which every edge has a direction from one vertex to another

Undirected graph

A graph in which every edge is symmetric

Cyclic Graph

A graph in which you can always find at least a path that starts and ends on a same vertex

Acyclic Graph

Can not find any path that starts and ends on a same vertex

Weighted graph

A graph in which every edge has a weight

Depth-first search (DFS, Graph)

Starting from one vertex, visit all vertices along the path started from the starting vertex till then end of the path (no unvisited neighbors) and then backtrack.

Breadth-first search (BFS)

Starting from one vertex, visit all other vertices in the order of the distances to the starting vertex.